On my recent trip to Fort Myers Beach, Florida, I set my astronomical observation goal to observe the nearest bright star, Alpha Centauri. Alpha Centauri is known to be 4.3 light years away. The really closest star is Proxima Centauri at 4.2 light years away, with a brightness of 10.43 – 11.11 magnitude. It is 2.18° southwest of Alpha Centauri in the sky, but a telescope would be needed to observe it.
Alpha Centauri has coordinates 14h 39m 36.49400s, −60° 50′ 02.3737″, J2000. Fort Myers Beach is located at about 26.4° north latitude and -82.2° longitude, so a (very bright) object with a declination of up to 90°-26.4°=-63.6° could be observed on the horizon. Thus, when passing through the local meridian, Alpha Cen can rise up to -60.8° – -63.6° = 2.8° high above the horizon without considering refraction. This is high enough above the horizon to allow for the observation of a star with a brightness of 1.3 magnitude. All of Florida is very flat and south of Fort Myers Beach there is the sea, so nothing should hinder observation except the weather.
And when is the best time to observe? After all, when the object is as high as possible above the horizon, i.e. it passes through the meridian. In that case, it has zero hour angle and the local sidereal time is equal to the astronomical right ascension of the object.
On the morning of January 24th I went out to the beach. In the southeast the constellation of Scorpion was rising. And in the south I recognized the constellation of Centaurus, which was unknown to me. Down low on the horizon were two fairly bright stars, Alpha Centauri / Rigil Kent and Hadar, easily visible to the naked eye. Here is a picture I took at 5:33 in the morning from the beach, unfortunately, the sea level here is not horizontal, it is inclined about 7 degrees. The image in the header of the article is annotated. To my surprise, the globular star cluster Omega Centauri (Caldwell 80) is easily visible. I saw three stars from the Southern Cross, but I couldn’t see the southernmost one Acrux even in 10×50 binoculars. But here in the 4s exposure it is faintly visible. Click on pictures for full resolution.
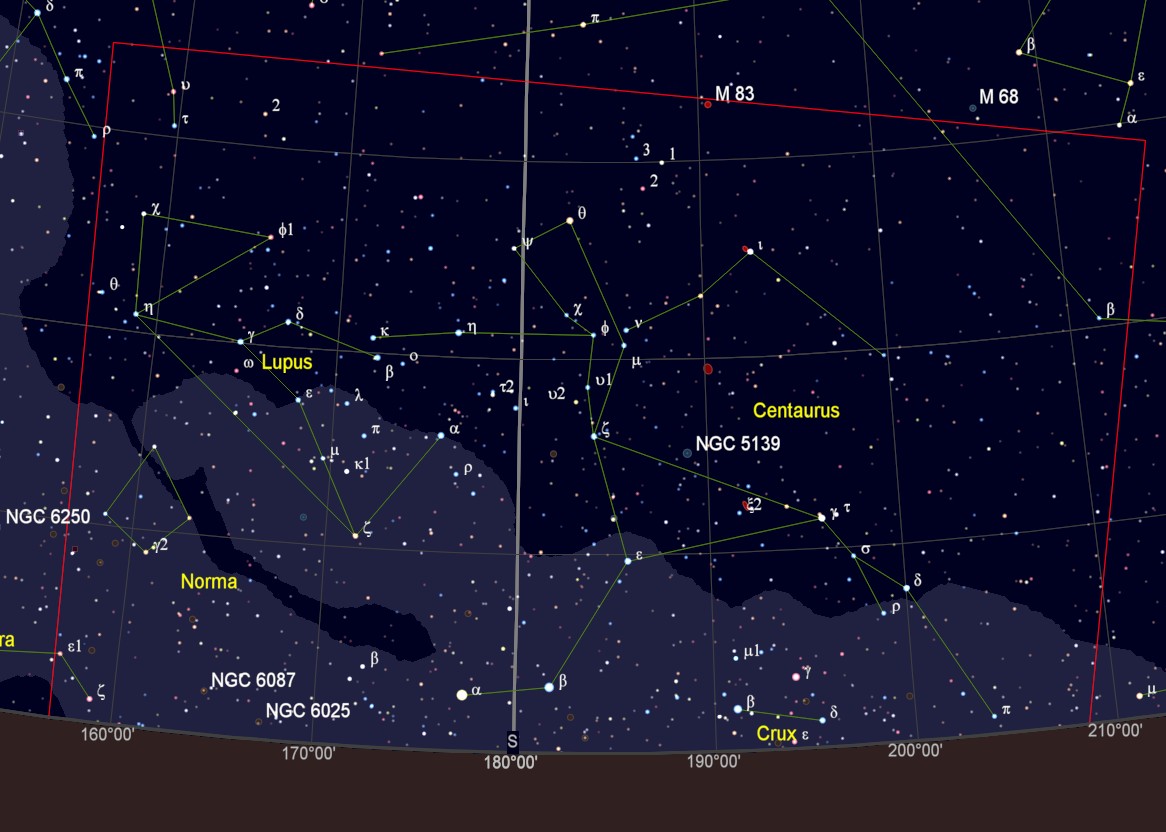Map of the image created by Jaromir Ciesla and here is an updated image.
Here are the formulas for calculating local sidereal time:
ha = LST - RA
ha = 0
#ha .. hour angle
#LST .. local star time
#RA .. right ascension
T = (JD0 - 2451545)/36525
#T .. current date in Julian centuries since the standard epoch (J2000.0)
#JD0 .. Julian date for the nearest preceding midnight of Universal Time (UT)
ST0 = 6.697374558 + T(2400.05133691 + T(0.000025862 -T(0.0000000017)))
#ST0 .. sidereal time at the prime meridian in Greenwich according to
the third-order approximation
LST = ST0+ 1.0027379093t1+l/15
#l .. the longitude of the observation site in degrees
-o-